

勾股定理是我们中学阶段学习的欧氏几何的发端,是欧氏几何的基础定理,有巨大的实用价值.勾股定理是历史上第一个把几何与代数联系起来的定理。勾股定理导致了无理数的发现。这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在高等数学和其他科学领域也有着广泛的应用.上个世纪,发行过一套题为“改变世界面貌的十个数学公式”邮票,这十个数学公式由著名数学家选出的,勾股定理是其中之首。

那么,到底勾股定理的内容是什么呢?
用语言描述:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。
用几何的符号语言说:如图,
∵∠C=90゜(或AC⊥BC)
∴在Rt△ABC中 a2+b2=c2(或AB2=BC2+AC2)
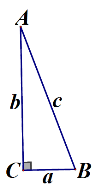
请注意,约定俗成,∠A所对的边是a,也可用BC来表示
同理,∠B所对的边是b,也可以用AC表示;∠C所对的边是c,也可以用AB表示。通常令∠C=90゜
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以我们称这个定理为勾股定理。可是,勾股定理还有许多其他名字,如“商高定理”,“毕达哥拉斯定理”,“百牛定理”。
公元前11世纪,周朝数学家商高就提出“勾三、股四、弦五”。《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”意为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,根据该典故勾股定理也被称为商高定理。
到公元3世纪,三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》中,“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。咱们数学课本(新人教版)的封面就是这个图的简化版,后人称其为“赵爽弦图”。东汉末年数学家刘徽根据“割补术”运用“青朱出入图”给出了勾股定理的几何证明。
公元前六世纪,希腊数学家毕达哥拉斯证明了勾股定理,因而西方人都习惯地称这个定理为毕达哥拉斯定理。据传说当年毕达哥拉斯定理发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又被称为"百牛定理"。根据考古资料,古埃及和古巴比伦人也会应用勾股定理。
千百年来,无数先贤用奇思妙想给出勾股定理的证明,如写几何原本的欧几里德,文艺复兴的全才达芬奇,第二十任美国总统加菲尔德,物理学家爱因斯坦,中国科学院院士张景中等等。积累至今日,据说已经有将近五百种证明方法。
下面,跟我一起看先贤们证明勾股定理的经典方法。
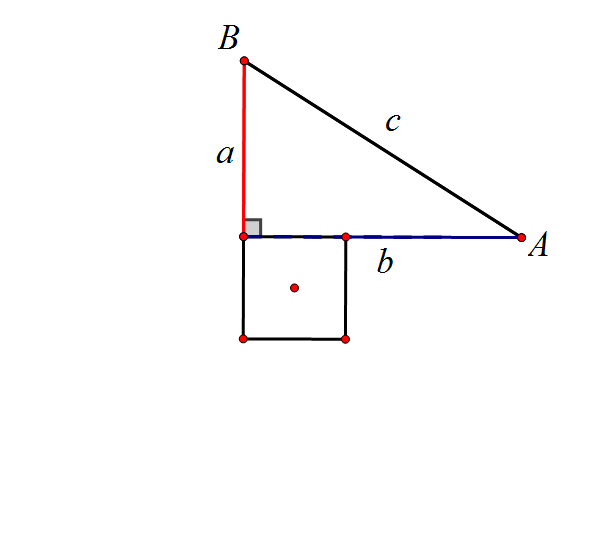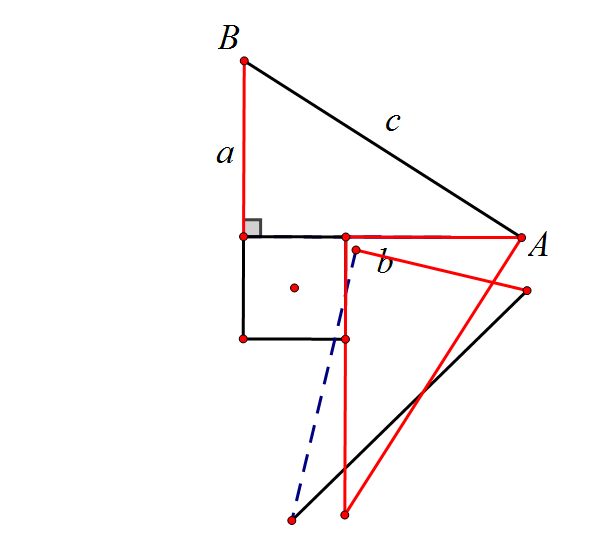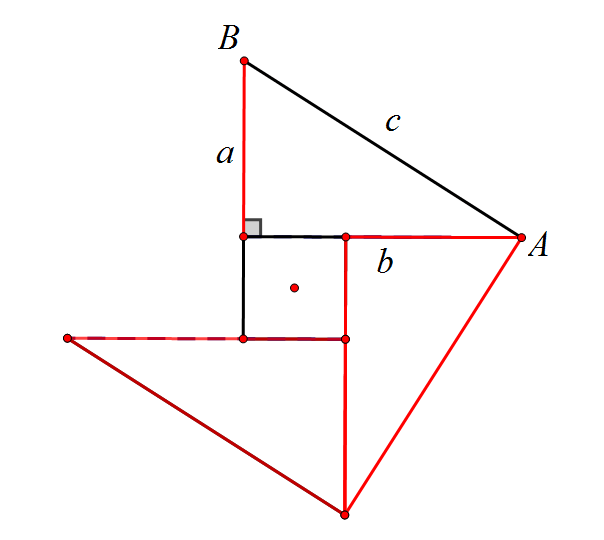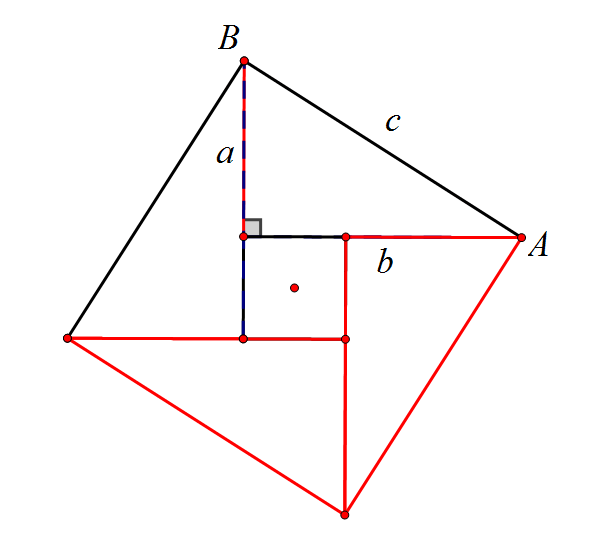
方法一,先看个有史以来图形最简洁的证明吧,这是美国第20任美国总统詹姆斯.加菲尔德的证法。下图中三角形ABC和三角形A'AC'全等且点A在线段CC'上。
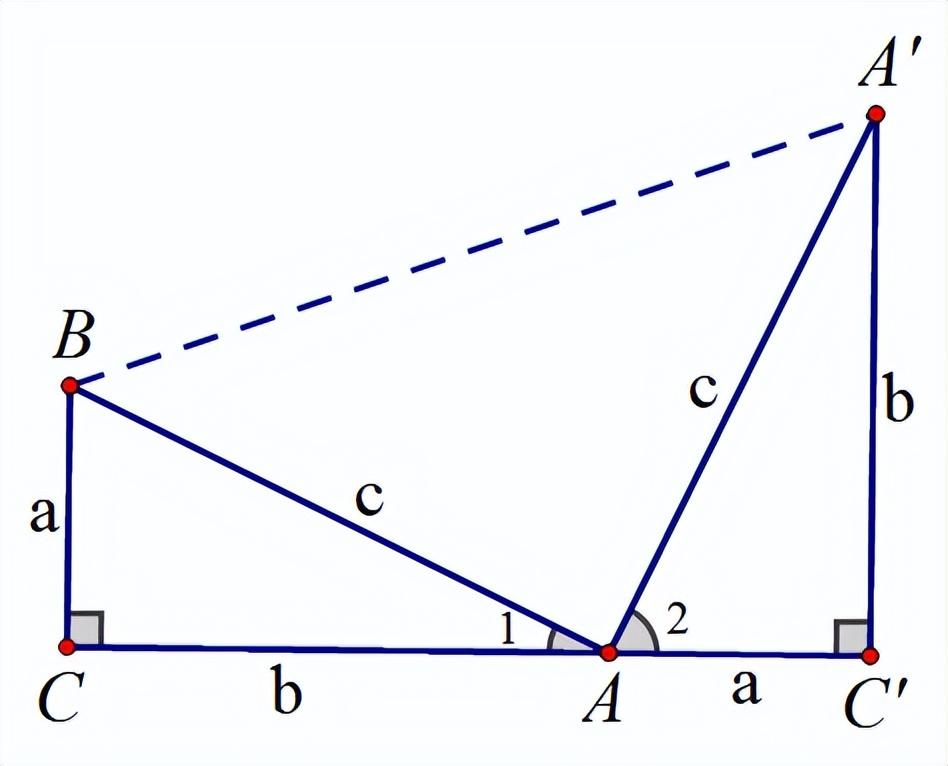
如上图,

把上图旋转180度,会得到证法二(邹元治法)
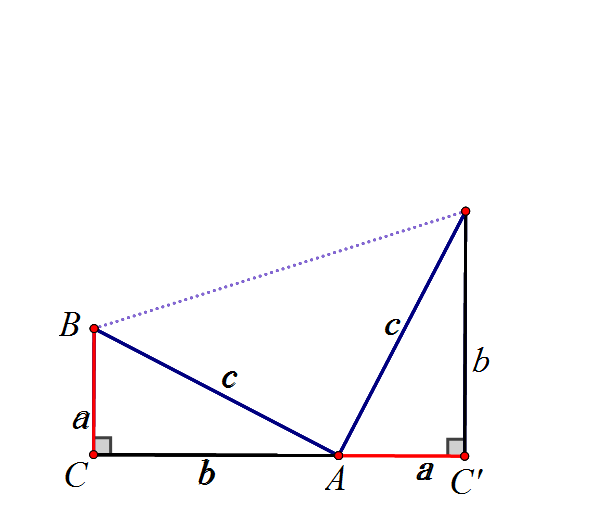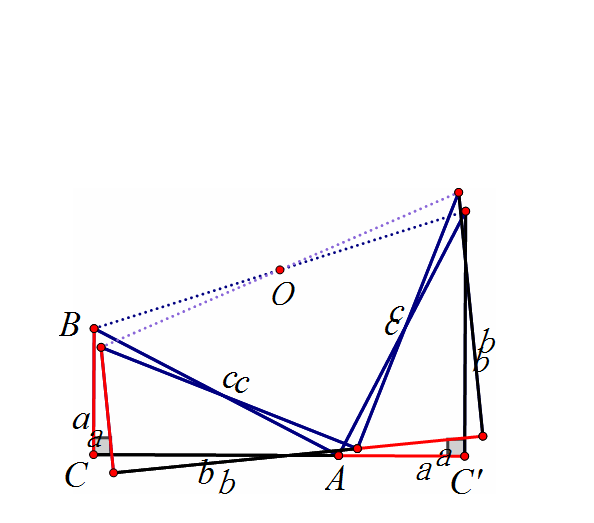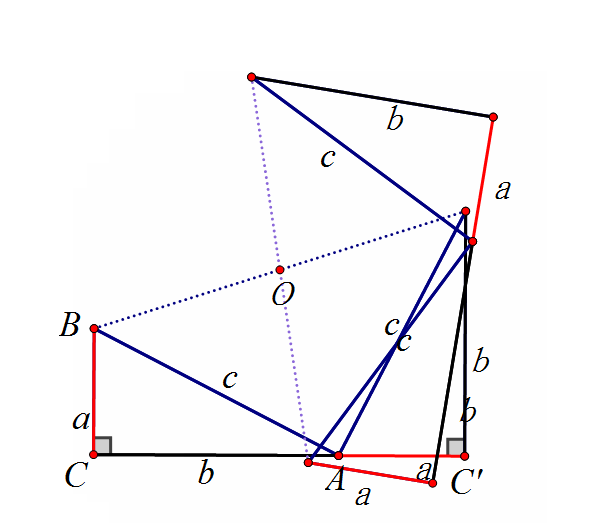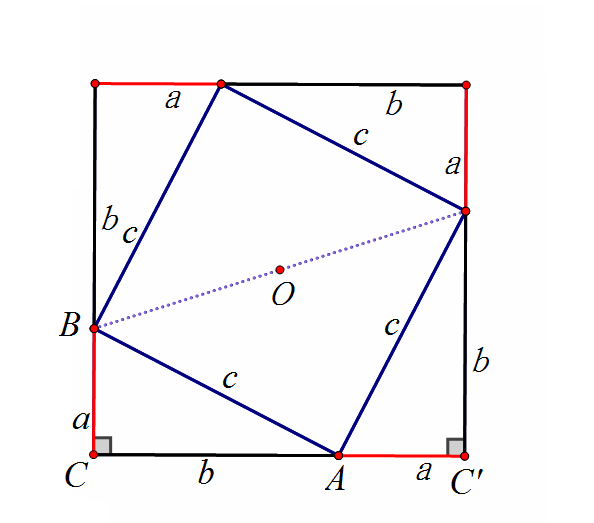

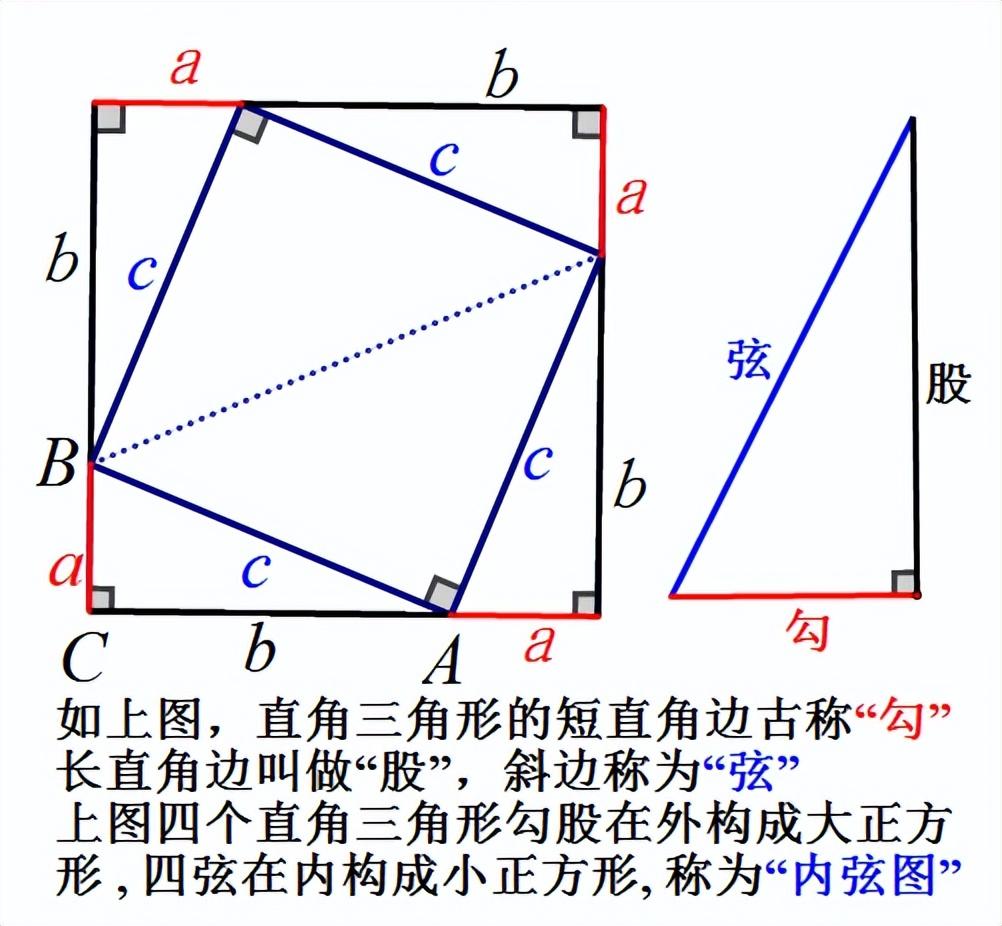
也有人认为内弦图证法是商朝时的数学家商高的证明方法。因为对《周髀算经》中古文的某些字的具体含义有不同的理解,研究数学史的教授们也对商周是证明了勾股定理还是仅给出了一组勾股数没有定论。
也可能用“内弦图”证明勾股定理比较简洁,历史上或许有太多人用这个方法给出了证明,“名可名,非常名”,叫商高法还是叫邹元治法其实也无所谓了。
证明方法三(外弦图)
先请看下面动态图
可以看出,一个勾为a,股为b的直角三角形绕边长为(b-a)的正方形旋转,可以得到一个以弦c为边长的大正方形。
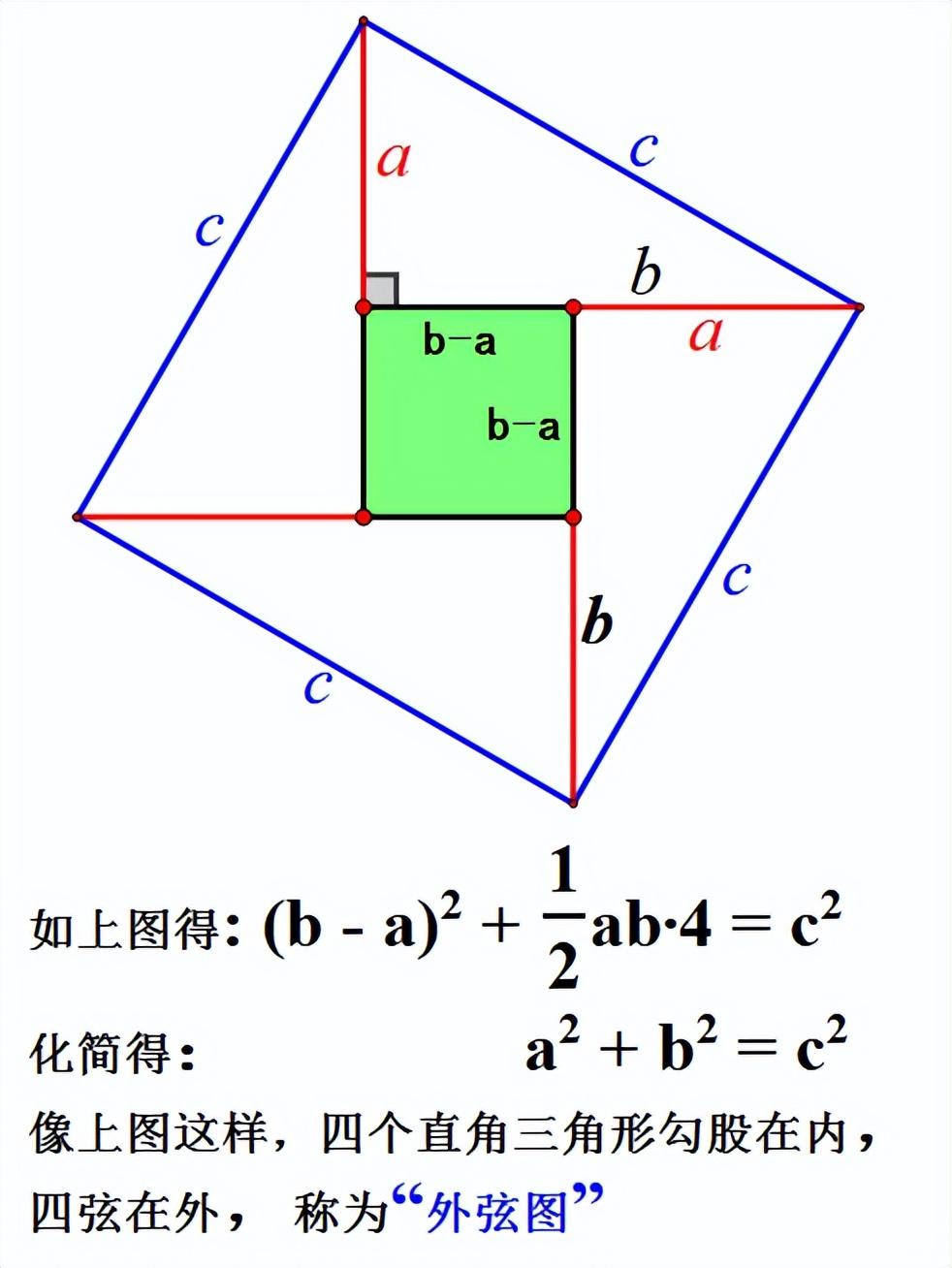
证明方法四(课本赵爽弦图)
赵爽,是三国时期吴国人。他在《周髀算经注》中给出“勾股各自乘,并之,为弦实。开方除之,为弦。”
还是先看动态图吧
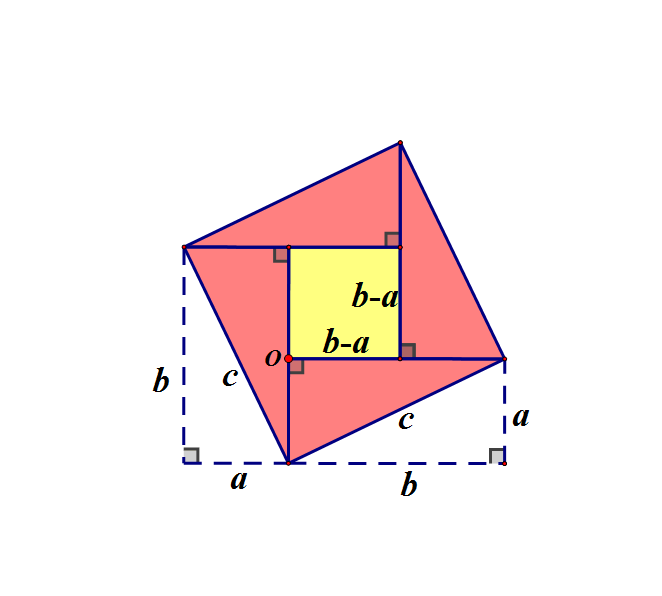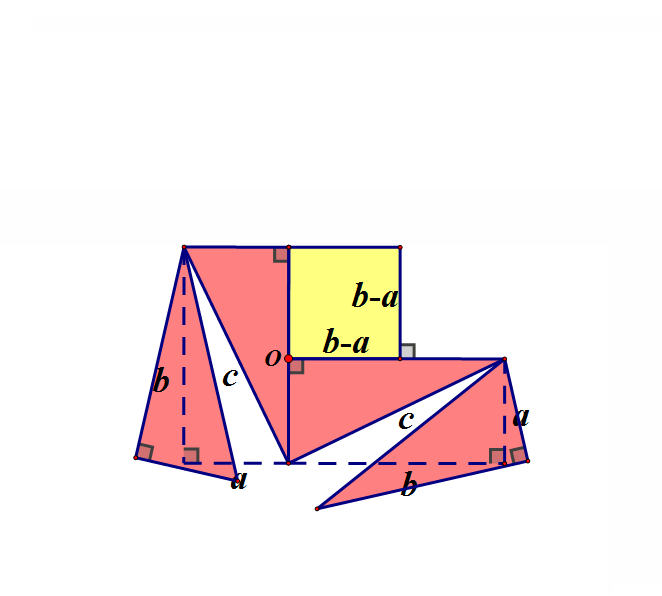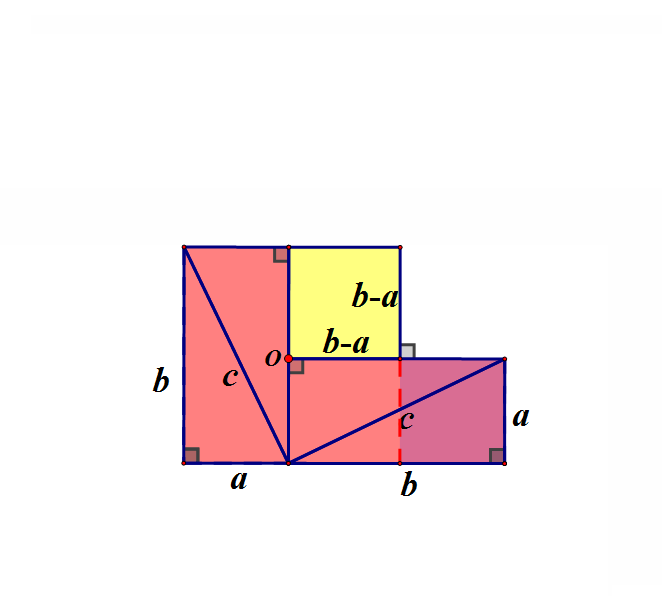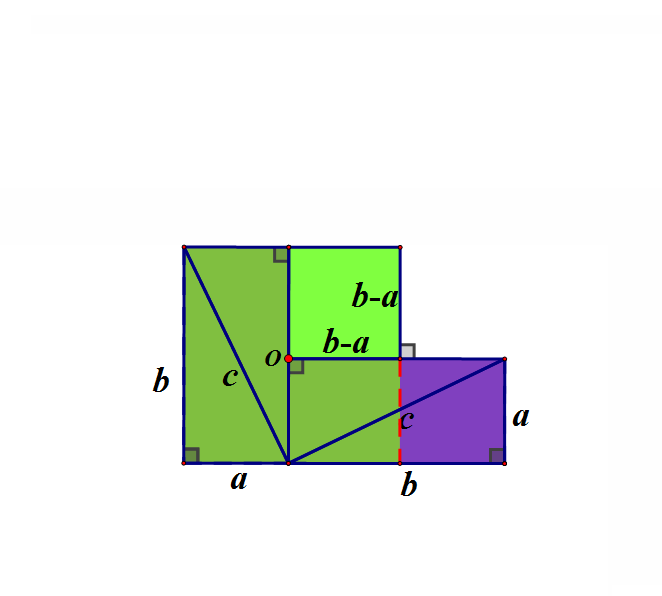
赵爽弦图其实就是换了证法的“外弦图”
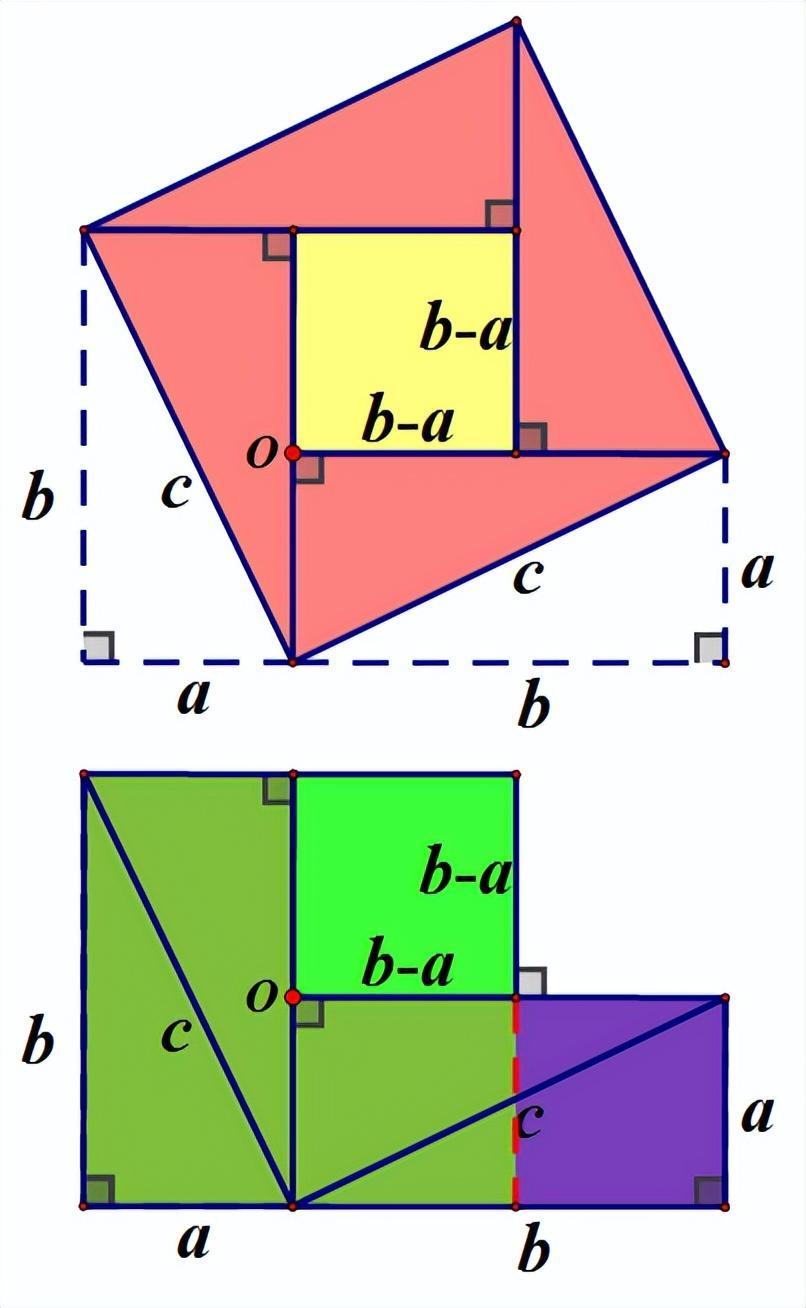
上图的四个“朱实”与一个“黄实”的面积和是边长为c的正方形的面积
旋转后得到下面的图,可重新组合成边长为b的正方形“绿实”再加上边长为a的正方形“蓝实”。
方法五:传说中的毕达哥拉斯的证法
不解释了,看动态图吧
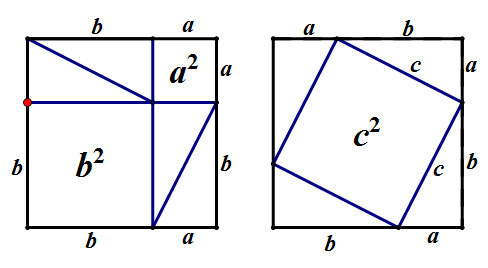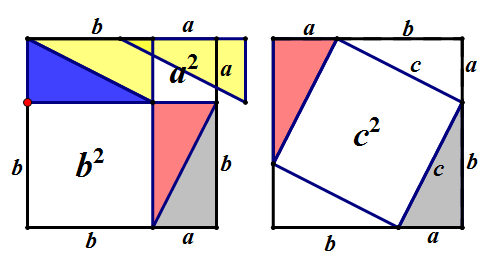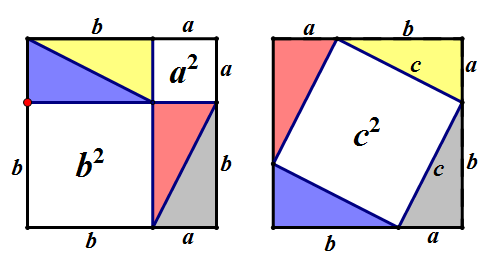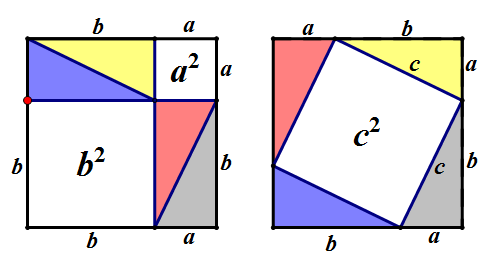
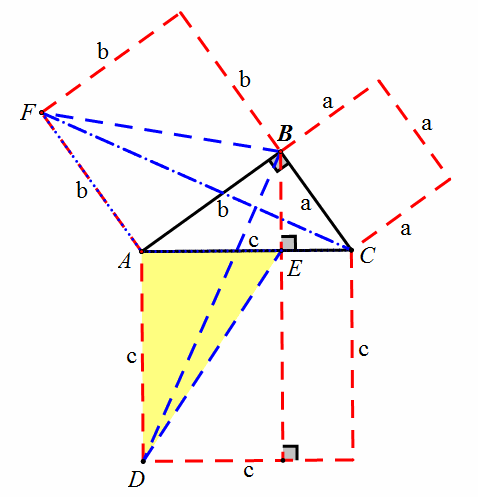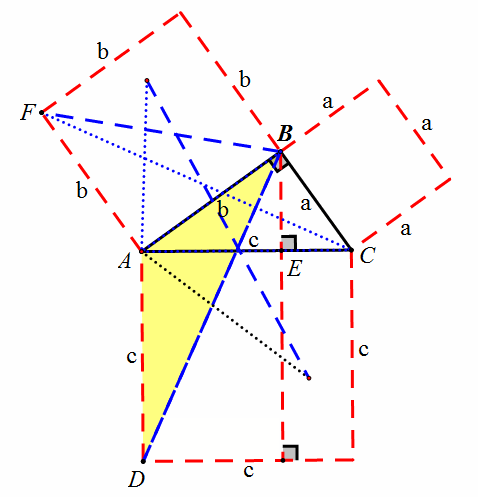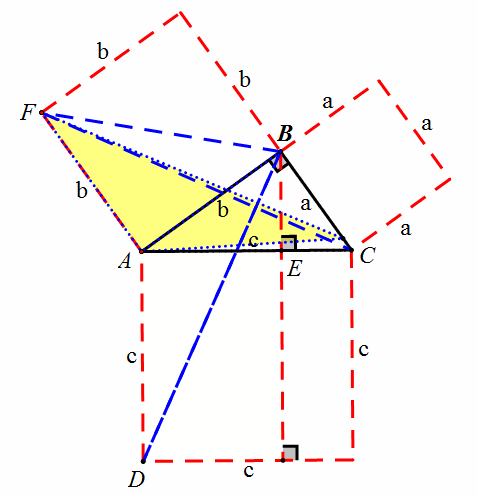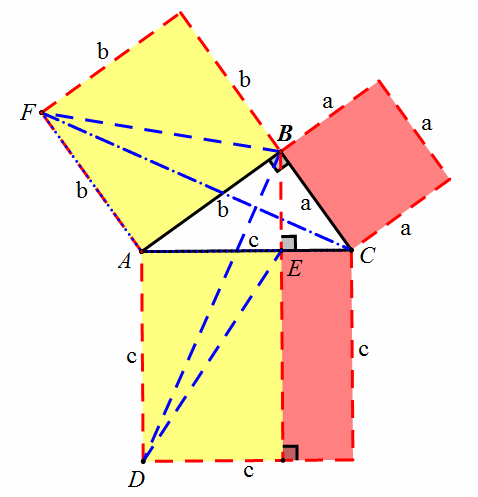
方法六:传说中欧几里得的证法

由同底等高可得三角形ADE和三角形ADB面积相等,由旋转重合可得三角形ADB和三角形ACF全等,由同底等高可知三角形ACF和三角形ABF面积相等。

请看动态无声证明
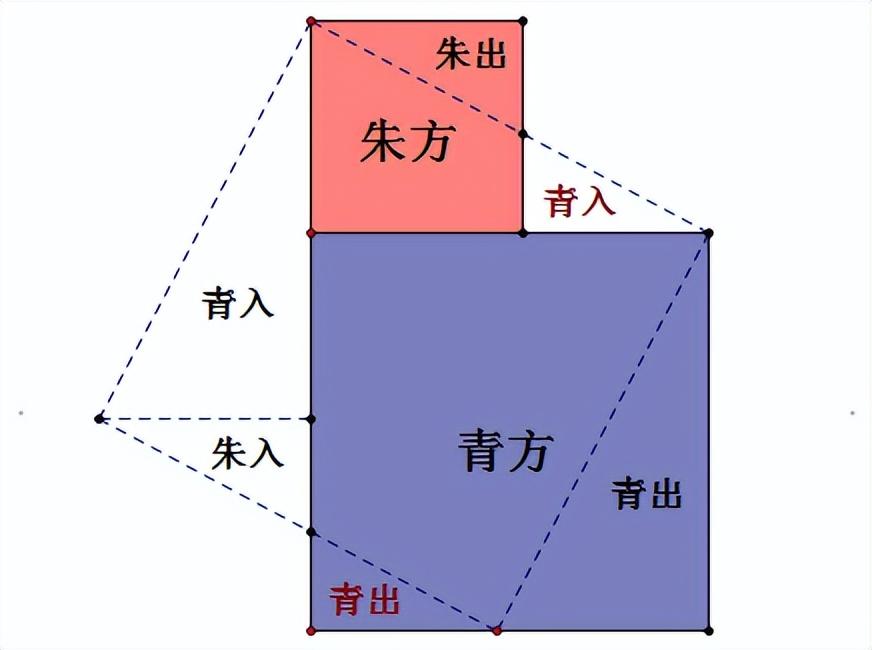
方法七:魏晋时期的数学家刘徽的青朱出人图
请看动态图
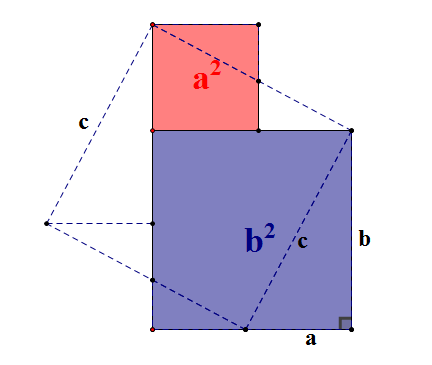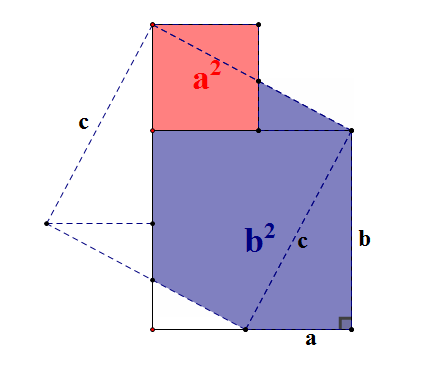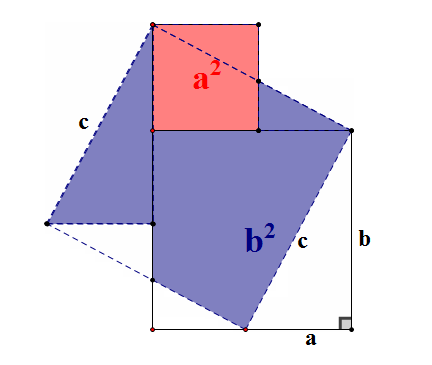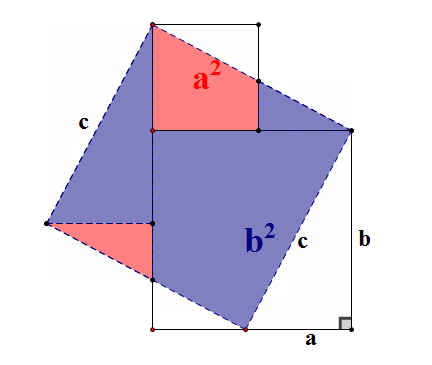
方法八:中科院院士张景中的证法
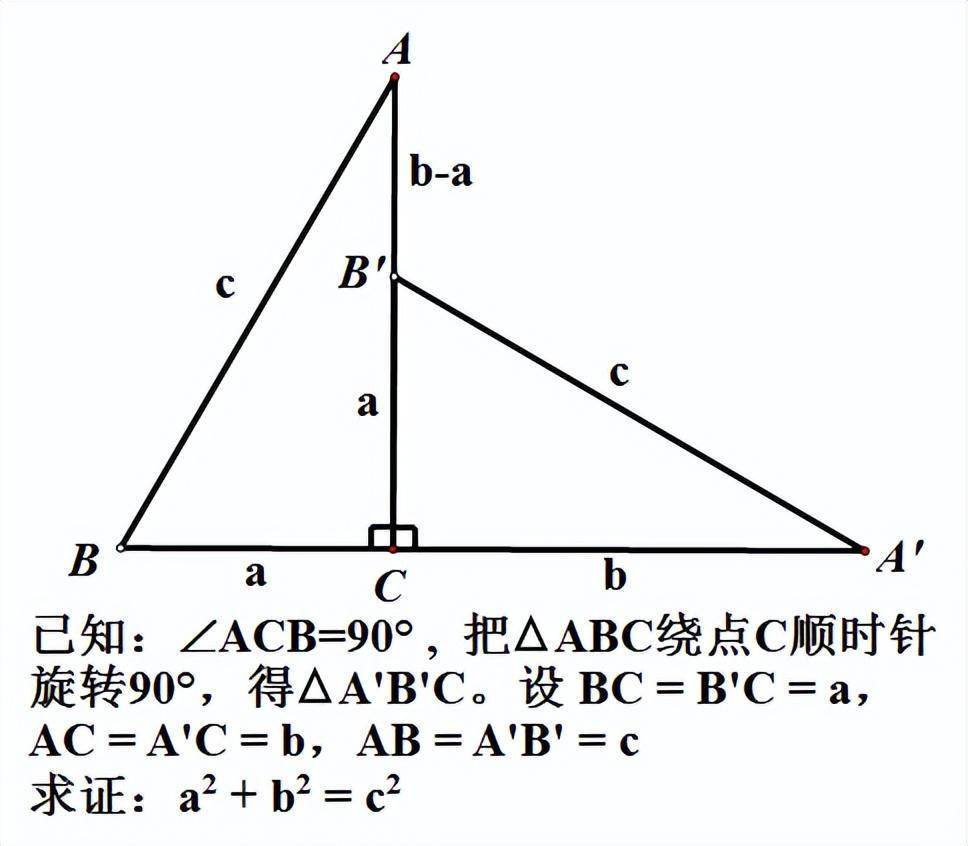
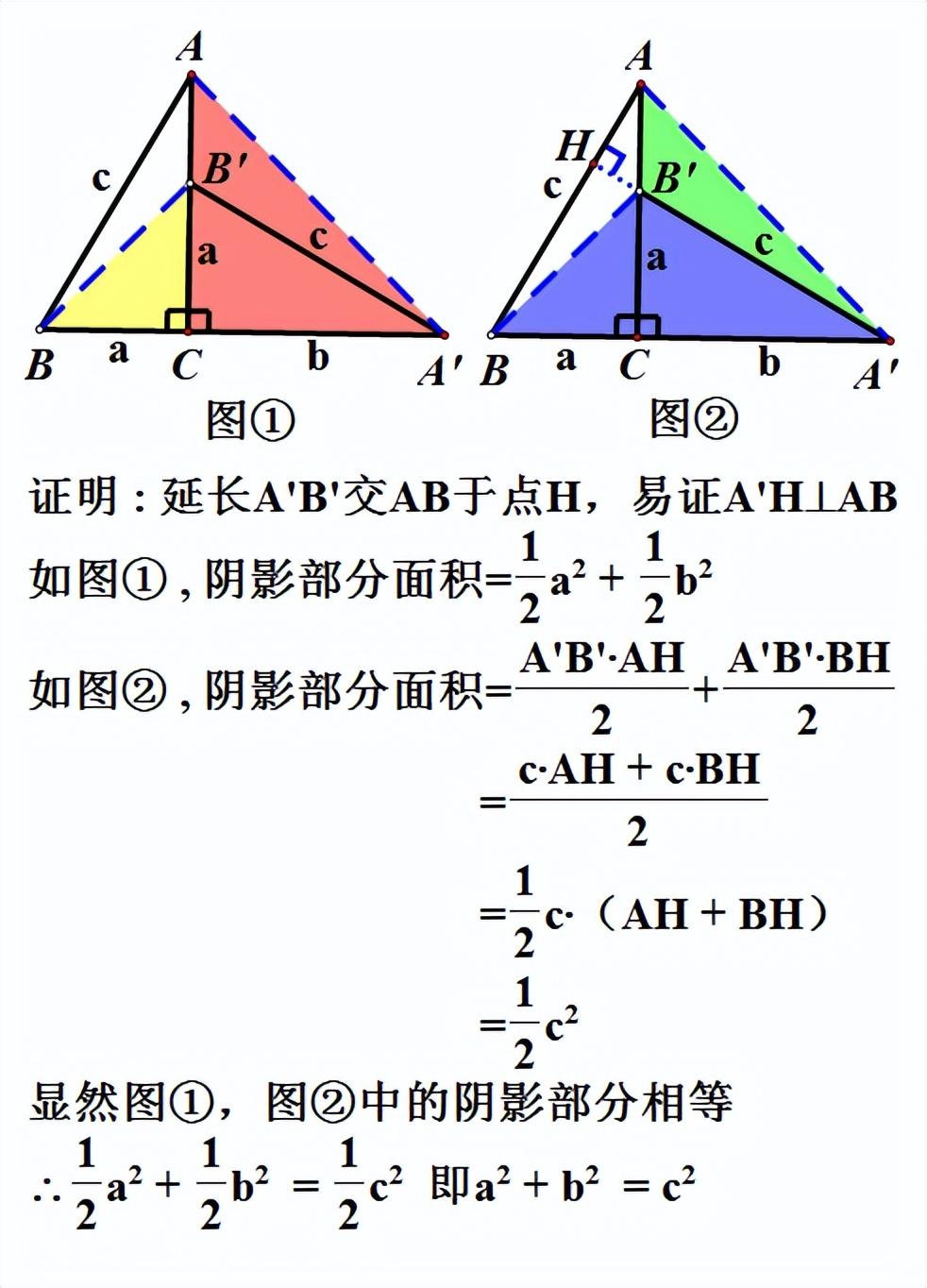
方法九:达 · 芬奇的证明方法
艺术家的证明过程看下面的动画就行了
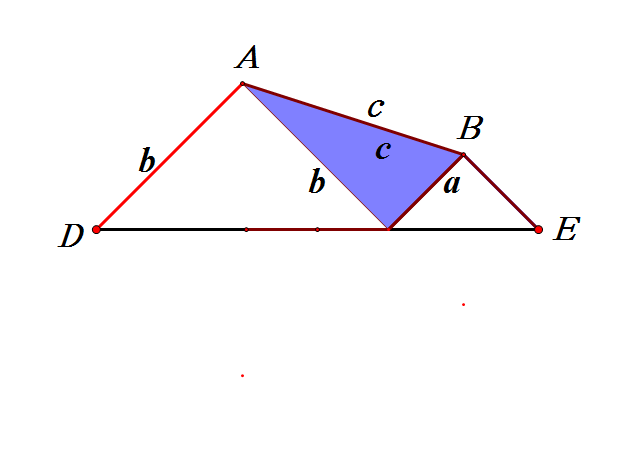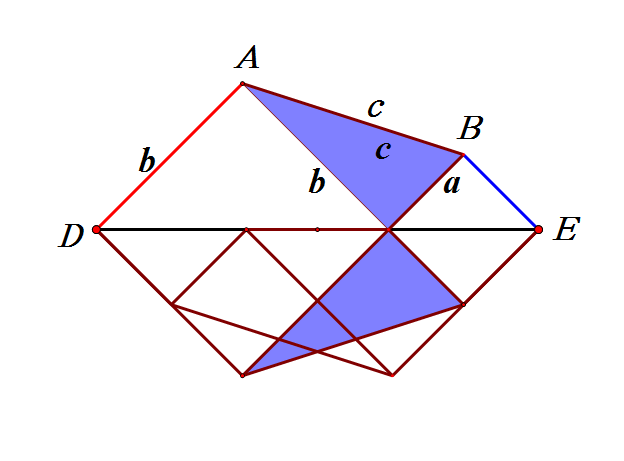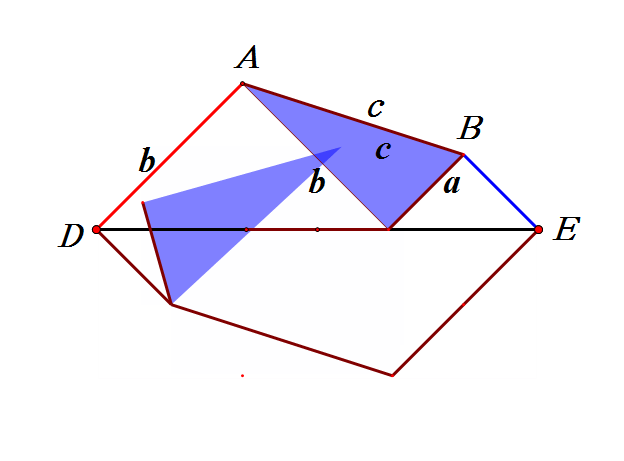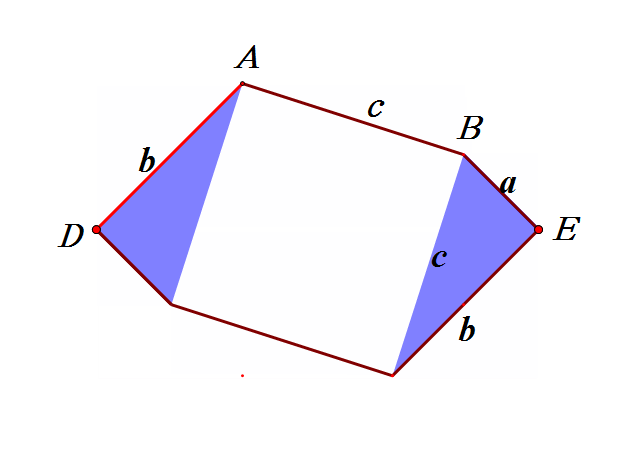
方法十:四边形面积的恒等变形法

下面的证明方法超出了八年级学生现阶段的知识掌握量,但九年级的学生还是能看懂的。
方法十一:射影定理法(双垂三相似)
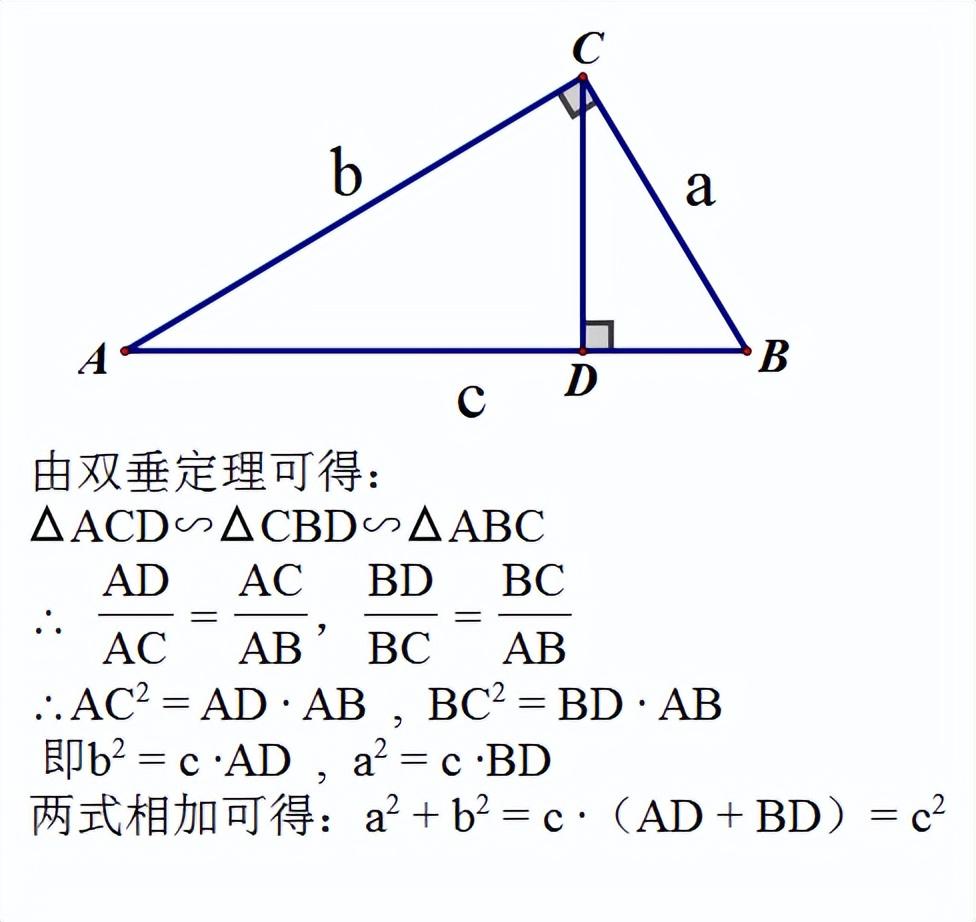
方法十二:爱因斯坦的证法
据说是爱因斯坦在十一岁的时候想出来的,为了书写过程方便,我把这个方法稍作了改动。
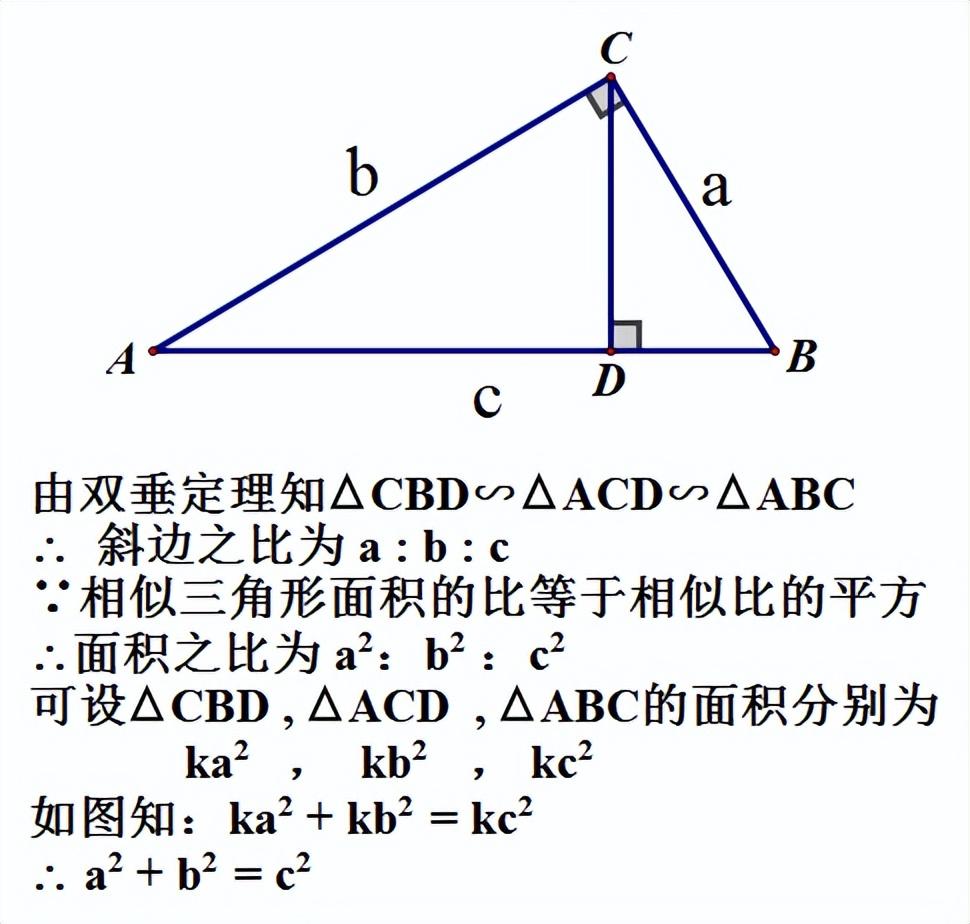
方法十三:(内切圆法)
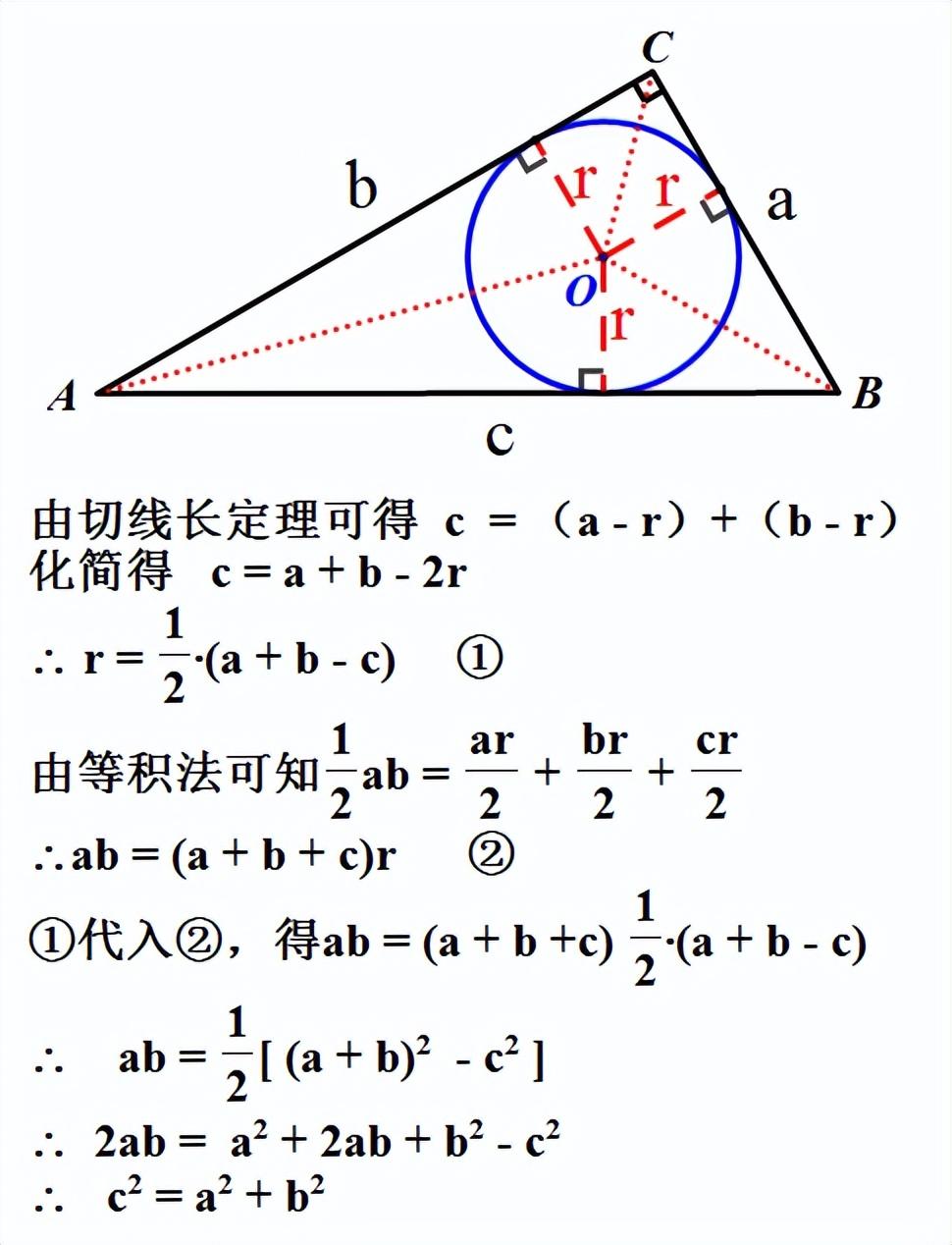
下面的方法九年级的学生知识储备也不够用了,但应该能看懂。我会把用到的定理提前说明。
方法十四:(切割线定理法)
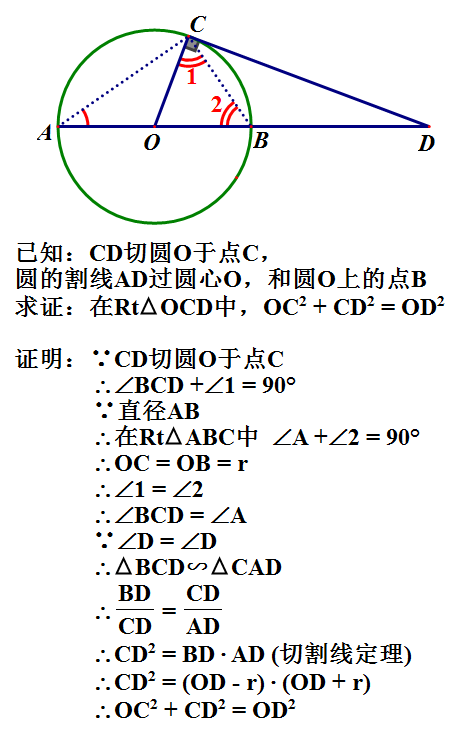
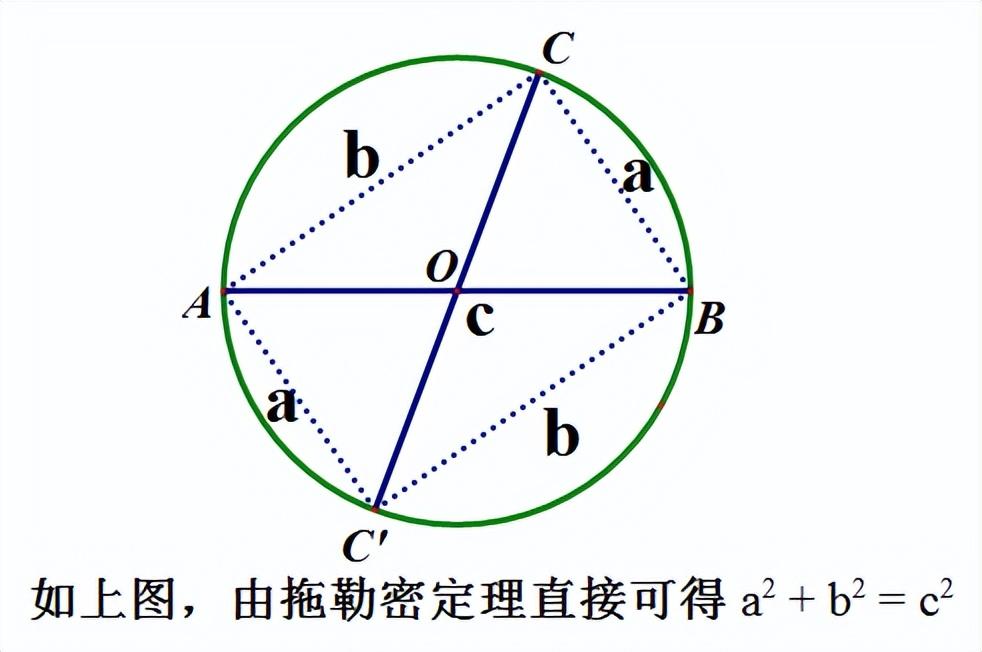
方法十五:拖勒密定理法(也有音译为多列米定理)
拖勒密定理:圆内接四边形两条对角线的乘积等于两对边乘积之和。这里写怎样证明了。
下面隆重推出方法十六,我看到梅文鼎,项明达,陈杰等人,都用如下右图来证明勾股定理,他们的证明仅构造图形的顺序和辅助线作法有区别。我效颦一下,请看我的想法。
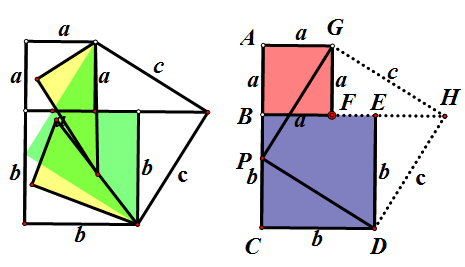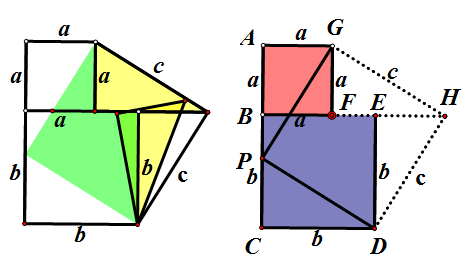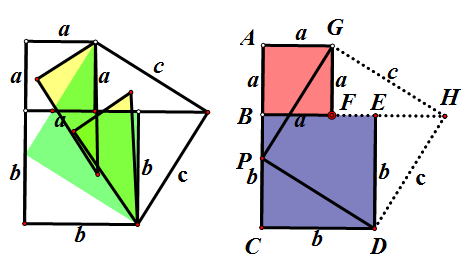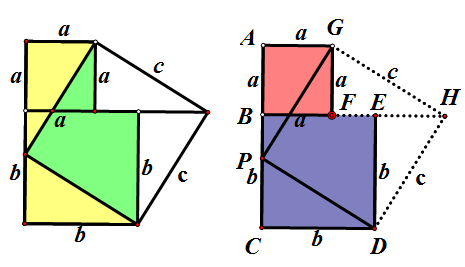
如上右图,构造边长为a,b的两个正方形,在线段AC上取点P,使AP=b,则CP=a,延长BF到点H,使FH=b,则EH=a,连接GH,DH。用SSS可证三角形APG和三角形FHG全等,同理三角形CDP和三角形EDH全等。所以,如上左图动画演示可证。